累積分布関数

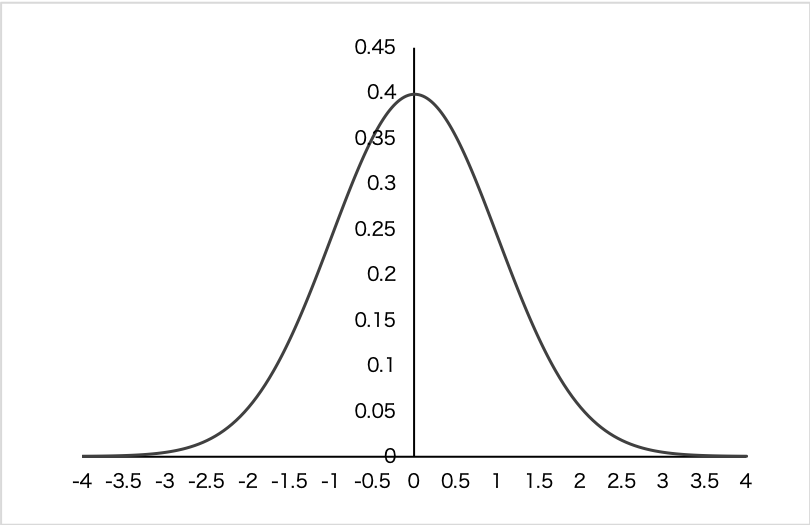
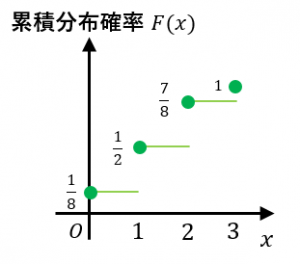
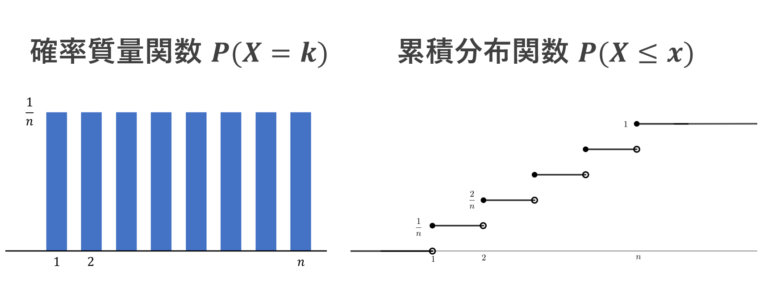
累積分布関数（るいせきぶんぷかんすう、英: cumulative distribution function, CDF）または分布関数（ぶんぷかんすう、英: distribution function）とは、確率論において、確率変数 X の実現値が x 以下になる確率の関数のこと。連続型確率変数では、負の無限大から x まで確率密度関数を定積分したものであるとも言える。

累積分布関数は同時確率分布でも条件付き確率分布でも定義される。

定義

実数値確率変数 X の累積分布関数は以下で定義される。この確率は下側確率 (lower-tail probability) とも呼ばれる。

${\displaystyle F_{X}(x):=\operatorname {P} (X\leq x)}$

X の a < b の時の半開区間 (a, b] の確率は以下になる。

${\displaystyle \operatorname {P} (a$

連続型確率変数の累積分布関数は確率密度関数が存在する場合は以下になる。

${\displaystyle F_{X}(x)=\int _{-\infty }^{x}f_{X}(t)\,dt}$

特徴

累積分布関数は広義単調増加関数であり、右連続関数である。さらに以下が成立する。

${\displaystyle \lim _{x\to -\infty }F_{X}(x)=0,\quad \lim _{x\to \infty }F_{X}(x)=1.}$

離散型確率変数 X では以下が成立する。

${\displaystyle F_{X}(x)=\operatorname {P} (X\leq x)=\sum _{x_{i}\leq x}\operatorname {P} (X=x_{i})=\sum _{x_{i}\leq x}p(x_{i}).}$

連続型確率変数 X では以下が成立する。

${\displaystyle F_{X}(b)-F_{X}(a)=\operatorname {P} (a$

派生関数

相補累積分布関数

相補累積分布関数 (complementary cumulative distribution function, CCDF) とは、以下で定義される関数。この確率は上側確率 (upper-tail probability) とも呼ばれる。

${\displaystyle {\bar {F}}_{X}(x)=\operatorname {P} (X>x)=1-F_{X}(x)}$

分位関数

分位関数 (quantile function) や分位点関数とは、累積分布関数が狭義単調増加で連続な場合に定義される累積分布関数の逆関数 ${\displaystyle F^{-1}(p),p\in [0,1]}$ のこと。逆関数サンプリング法などで使用される。正規分布の場合はプロビットという。

参照